Diversificazione e portafogli efficienti: come tenere in tasca la certezza

La notorietà della relazione tra rendimento di un asset e il rischio verso cui si incorre detenendolo è ormai di ampio spettro conoscitivo. Lo è talmente tanto che tale principio ha istituito delle solide basi teoriche per la valutazione e confronto di titoli con caratteristiche diverse e utile a comprendere la diversificazione di portafoglio.

Diversificazione: perchè così importante?

La diversificazione, pratica attraverso cui gli investitori tentano di ridurre il rischio di portafoglio attraverso la detenzione di un sempre maggior numero di strumenti finanziari, è la keyword che lega rendimento e volatilità. Il tentativo di operare nel modo più sicuro possibile tra i meandri dei mercati, ha reso possibile la costruzione di diversi modelli valutativo-predittivi, basati su analisi quantitative e di stima. Detenere un pacchetto azionario diversificato permettere la realizzazione e il raggiungimento di risultati mediamente più affidabili in termini di performance, assicurando rendimenti perlopiù positivi. Questo perché le oscillazione dei prezzi delle azioni – causati ad esempio da shock di mercato imprevedibili come l’inflazione – non hanno un andamento uniforme; di conseguenza la mission prioritaria degli investitori “intelligenti” – citando Graham – è quella di ottenere un differenziale quanto meno positivo, risultato dei rendimenti medi contenuti nei loro portafogli, al netto delle oscillazioni degli indici dei mercati finanziari.

Come determinare il tasso di rendimento di un portafoglio azionario?

Generalmente il tasso di rendimento di un portafoglio è un valore che spiega la remunerazione ottenuta dall’ammontare delle scelte d’investimento effettuate su un portafoglio azionario; è dato – nel caso di due attività finanziarie, x e y – dalla somma tra il prodotto della percentuale di portafoglio investita nell’azione x per il tasso di rendimento specifico di x e il prodotto della percentuale di portafoglio investita su y per il tasso di rendimento specifico di y. 

Se quindi si volesse investire il 40% del valore di un portafoglio in azioni Tesla, per cui si prevede un tasso di rendimento atteso del 3,15% e il restante 60% in azioni IBM, con un tasso di rendimento atteso del 2,12%, il rendimento atteso di portafoglio sarà pari a:

Rp= (0,0315 X 40) + (0,0212 X 60) =2,532%  

La diversificazione della composizione di pacchetti azionari ha quindi come obiettivo finale la minimizzazione del rischio; assumendo una funzione di copertura degli investimenti effettuati attraverso la compensazione degli sbalzi di prezzo, se ad esempio da una parte l’indice x potrebbe subire un calo drastico per qualsiasi ragione, d’altro canto un possibile aumento dell’indice y potrebbe lenire le perdite complessive.

Un maggior numero di azioni detenute diminuisce il rischio, ma non sempre è così

Appunto importante da menzionare riguarda una particolarità sulla relazione che lega il numero dei titoli contenuti in un portafoglio azionario e la volatilità stessa; la diversificazione dimostra infatti che all’aumentare del numero di titoli detenuti, il rischio tenda ad abbassarsi, ma fino ad un certo punto; quando infatti subentra il rischio, è necessario scindere questa variabile in due componenti, in quanto non è detto che la probabilità che il prezzo di un indice azionario collegato ad un’azienda crolli solo ed esclusivamente per colpa delle perfomance di quest’ultima, essendoci una moltitudine di fattori e cause delle oscillazioni.

Si andrà quindi a discutere di rischio sistematico quando si fa riferimento a quella frazione di rischio imputabile a fattori economici e che non è direttamente collegata alle scelte d’investimento; questa componente di rischio è generata principalmente da disordini del mercato azionario e ravvisabile quando lo shock improvviso colpisce interi settori. Parleremo di rischio specifico quando la componente volatile è direttamente imputabile alle scelte di portfolio.

Il contributo di Markowitz

Il premio Nobel Harry Markowitz ha contribuito alla realizzazione di modelli teorici utili a comprendere come dover agire in controtendenza rispetto alle oscillazioni degli indici azionari, arrivando alla costruzione di modelli efficaci nel determinare il valore del miglior possibile rendimento di un portafoglio, considerata la variabilità – che è una misura del rischio e indica il grado di dispersione dei rendimenti di un asset attorno ad un valore medio – dei titoli stessi, concependo i  suddetti “portafogli efficienti”. Un portafoglio azionario viene definito efficiente quando la sua composizione è tale da minimizzare il rischio e massimizzare il rendimento complessivo, risultante dalla miglior combinazione possibile di N azioni su cui s’intenderebbe investire.

Rendimento atteso del portafoglio e varianza sono due misure utili a determinare l’allocazione più efficiente rispetto a un variegato paniere di azioni. L’analisi da effettuare è utile a determinare in primis il così detto “premio atteso per il rischio”, meglio noto come il costo-opportunità sopportato per il mancato investimento in un’attività risk free – come i BOT – e quindi specularmente è il rendimento atteso per l’impegno assunto nell’aver investito in un titolo azionario contrassegnato da un medio/alto livello di rischio, rinunciando ad attività che ne sono prive.

Per la determinazione del rendimento atteso appena menzionato e della migliore assets allocation, si ricorre generalmente al Capital Asset Pricing Model, noto come CAPM.  

Diversificazione, covarianza e correlazione: come si misura il grado di rischio di un portafoglio?

Ai fini della determinazione del premio per il rischio ottimale, dato un paniere di attività finanziarie, è necessaria l’analisi dei valori che specificano il grado di rischio che detti strumenti inglobano.

La covarianza è un utile strumento di misurazione del rischio di portafoglio che permette di stimare l’andamento di due azioni messe a confronto e determina il grado di dipendenza di strumenti finanziari indirettamente correlati. Ricordando che il rendimento atteso di un portafoglio non è altro che la media ponderata dei rendimenti attesi dei singoli strumenti finanziari, la covarianza permette di stabilire con quale intensità la stima dei rendimenti specifici si discosta dalla stima del rendimento di portafoglio nel suo insieme. Per il calcolo della covarianza, è però necessario tenere in considerazione il coefficiente di correlazione, che permette di stabilire come le componenti del pacchetto azionario detenuto si muovano nel tempo. Parleremo infatti di correlazione:

• positiva, quando il valore ottenuto è > 0 e l’andamento è di conseguenza tendente all’essere uniforme
• negativa, quando < 0 e gli indici si muovono in direzioni opposte
• assenza di correlazione, se è pari a 0 e vi è indipendenza tra i valori

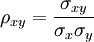
Tale variabile, compresa tra -1 e 1, non è altro che il rapporto tra la covarianza e il prodotto delle deviazioni standard degli indici azionari. E’ facile comprendere che il grado di rischio andrà a diminuire tanto quanto questo valore si approssimerà o andrà a superare negativamente lo zero.

Trend di mercato e composizioni di portfolio

Osservando i dati sui rendimenti medi per la stima di quelli attesi e avendo calcolato le varianze degli indici azionari da confrontare, è possibile determinare – secondo l’avversione al rischio e il target di remunerazione che l’investitore vuole raggiungere –  quella che Markowitz definì come “frontiera efficiente”, cioè il luogo dei punti delle possibili combinazioni di assets, secondo coefficienti di rischio e rendimento.

I punti situati sulla frontiera efficiente rappresentano quelle combinazioni di portfolio che offrono – date le preferenze del singolo – una combinazione tra rischio e rendimento ottimale; tutti i punti al di sotto della curva, sono combinazioni di portfolio definite inefficienti, come Buzzi Unicem, che presenta un rendimento moderato e un alto rischio. La finalità dell’individuo razionale è cercare di collocarsi nella sezione – immaginando quattro quadranti che dividono il grafico – più in alto e a sinistra possibile, in modo tale da massimizzare i profitti delle attività detenute e sincerarsi di un’adatta copertura.