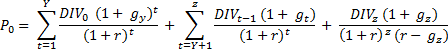Investire in azioni: il quadro degli indicatori di natura finanziaria

investire in azioni
Gli indicatori di natura finanziaria del rendimento e del prezzo delle azioni sono costruiti con riferimento alle stesse regole generali relative agli indicatori del rendimento delle obbligazioni. Nel dettaglio, il procedimento finanziario che verrà seguito è quello dell’attualizzazione e il regime finanziario che verrà eseguito è quello dell’interesse composto. Durante l’articolo, verranno proposte sempre più ipotesi semplificatrici che coniugheranno la rigorosità dell’impostazione teorica con la praticità di questi indicatori.
Scopriamo insieme di cosa si tratta.
Indicatore elementare su un orizzonte uniperiodale
L’indicatore elementare R1 si fonda sulla valutazione dei dividendi attesi e del prezzo di realizzo facendo riferimento ad un orizzonte temporale pari a 1. Il vantaggio di questo indicatore è quello dell’immediatezza poiché è semplice individuare la valenza positiva o negativa a seconda del valore di P1. Di fatti se si tratta di una valore maggiore di P0 avrà un risultato negativo e viceversa. La formula è:

Oltre al pregio dell’immediatezza poc’anzi esplicitato, questo indicatore ha un limite di non poco conto: considerando un holding period pari all’unità, non tiene conto dei frutti intermedi per interesse e per capitale. R1 però,può anche essere considerato come quel tasso che rende verificata l’uguaglianza tra prezzo P0 e la somma dei valori attuali dei frutti attesi nel periodo. In questo caso, l’indicatore non è altro che un normale tasso di rendimento a scadenza, dove quest’ultima è fissata ipoteticamente a 1.
Avremo quindi:
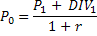
Indicatore completo su un orizzonte temporale completo
L’indicatore R2 tende a superare il limite del R1. L’indicatore è detto “completo” poiché prende in considera l’insieme dei flussi finanziari attesi: per questo bisogna determinare i prezzi al tempo 0 e dei successivi periodi fino al periodo k. Nel dettaglio avremo:
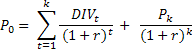
Anche in questo caso avremo un tasso di rendimento a scadenza ma essa va a coincidere con un periodo indeterminato k, coerente con la scadenza indeterminata dell’investimento azionario. Ma è proprio questo aspetto a renderlo ineccepibili da un punto di vista teorico ma inapplicabile nella realtà.
Indicatore semplificato legato alla logica del dividend discount model
Come detto in precedenza, i limiti dell’indicatore R2 riguardano la difficoltà di prevedere su un orizzonte temporale indeterminato i flussi relativi ai dividenti attesi ed il flusso relativo al prezzo finale: le semplificazioni possibili non possono che interessare questi due aspetti.
Per quanto riguarda il prezzo finale, l’ipotesi di semplificazione si fonda sul fatto che il prendere a riferimento un orizzonte temporale indeterminato equivale a immaginare un k tendente a infinito e quindi un valore attuale del flusso per capitale tendente a zero. Avremo quindi:

Essa rappresenta la veste formale alla base della logica dei dividend discount models spiegano il prezzo delle azioni con riferimento alla sola componente per dividendi e arrivano a definire tale prezzo come la somma del valore attuale dei dividenti attesi.
Ma anche qui abbiamo un limite che non possiamo trascurare: riguarda appunto l’ipotesi che esclude la componente capitale. Anche se, considerati holding period medio-lunghi, il valore attuale della componente capitale andrà ad abbassarsi, mentre il valore attuale della componente dividendi aumenterà visto il cumularsi degli stessi.
Investire in azioni: Ecco l’indicatore ancor più semplificato collegato alla logica del constant growth discount model.
Il modello in questione si fonda, come appare chiaramente dalla sua denominazione, sulla ipotesi che i dividendi futuri crescano a un tasso annuo costante g in presenza di un tasso di attualizzazione r superiore al suddetto tasso di crescita g.

Avremo quindi una rendita perpetua con un VAN pari a:

Possiamo dire quindi che il constant growth dividend discount model richiama la logica della rendita perpetua a capitale crescente dove per DIV 1 intendiamo i dividenti attesi al tempo 1, per g il loro tasso di crescita costante annuo e con r il tasso di attualizzazione per cui:

Questa formalizzazione si fonda quindi sull’ipotesi che il tasso di attualizzazione r sia sempre maggiore del tasso di crescita dei dividenti g ed è per questo che per valori r < g la progressione risulta priva di significato economico. Dalla relazione, però, è possibile ottenere il rendimento atteso, noti la stima dei dividendi attesi al tempo 1 il loro tasso di crescita costante e il prezzo iniziale della azione:
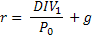
Investire in azioni: Indicatore di rendimento sofisticato collegato alla logica dei modelli a stadi
La limitata capacità applicativa del modello a crescita costante ha indotto gli analisti ad adottare modelli più complessi di valutazione dei titoli azionari i quali ipotizzano diversi tassi di crescita dei dividendi in corrispondenza delle diverse fasi del ciclo di vita dell’impresa. Le soluzioni possibili sono diverse, andando da quelle più articolate, che prevedono 4 o 5 stadi e, con riferimento allo stadio o agli stadi iniziali, una previsione puntuale di g, a quelle più semplificate, che prevedono un numero minore di stadi e una previsione meno analitica di g.
Esso ipotizza tre diverse fasi nel ciclo di vita dell’impresa i cui titoli azionari sono presi e per cui hanno un diverso valore di g:
- Prima fase, detta di stabilizzazione, si contraddistingue per un andamento del tasso di crescita dei dividendi g costante e per una durata relativamente breve, intorno ai 5 anni.
- Seconda fase, detta di transizione, si caratterizza per un andamento di g decrescente e per una durata media circa intorno ai 7 anni.
- Terza fase, detta di maturità, presenta un andamento di g nuovamente costante e una durata indeterminata, in pratica estesa ad un orizzonte temporale infinito.
Da qui: