I paradossi dell’economia: Ellsberg’s paradox
Qualsiasi studente di economia, almeno una volta nella vita, ha sentito parlare di economia sperimentale. Sempre con la stessa frequenza, abbiamo sentito parlare della teoria dell’utilità attesa e delle ipotesi su cui essa si fonda.
La teoria dell’utilità attesa
La teoria dell’utilità attesa descrive il comportamento degli agenti dinanzi ad una scelta: in particolare, gli agenti economici scelgono, sotto ipotesi di razionalità, di massimizzare l’utilità attesa derivante da un certo valore monetario e non il valore monetario stesso. Come calcolare l’utilità attesa? Semplicemente, moltiplicando l’utilità attesa di un valore X per la probabilità di ottenerlo. Ma non finisce qui: l’utilità attesa sarà la somma di tutti questi prodotti. Graficamente:
EU= E(x)p(x)+E(y)p(y)+E(z)p(z)
dove x,y,z sono 3 possibili vincite e p rappresenta la probabilità di ottenerle.
Si possono violare le ipotesi della teoria dell’utilità attesa?
Banalmente, le ipotesi alla base della teoria dell’utilità attesa sono quelle alla base della teoria dell’utilità classica, più una (almeno):
- completezza
- transitività
- continuità
- indipendenza
Come spesso accade in economia, se c’è un’ipotesi alla base di un modello, ci sarà anche modo di violarla. Ecco, infatti, che succede col paradosso di Ellsberg.
Il paradosso di Ellsberg
Facendo, in breve, un piccolo spoiler del finale, il paradosso di Ellsberg dimostra che gli individui violano le ipotesi alla base della teoria dell’utilità perché non si rispetta la transitività. Il paradosso di Ellsberg è sviluppato in due modi: con un’urna e con due urne, il primo è molto più noto ed immediato. Il secondo richiede l’applicazione di strumenti come l’integrale di Riemann e di Choquet. Per ora, tratteremo solo il primo.
Il paradosso di Ellsberg con una sola urna
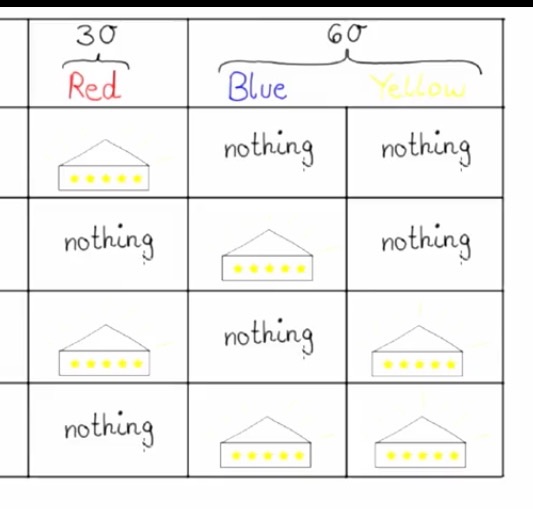
Immaginiamo che valgano tutte le ipotesi alla base della teoria dell’utilità attesa: siamo agenti razionali, con preferenze ordinate, complete, transitive ed indipendenti. Abbiamo, dinanzi a noi, un’urna contenente 90 biglie: 30 rosse e 60 nere e gialle. Tutti gli eventi sono equiprobabili. Ci vengono proposte due scommesse: al primo “turno” possiamo scegliere di puntare su X o Y. X è l’evento per cui se esce una biglia rossa, vinciamo 100euro. Y ci dà 100 euro se esce una biglia nera. Al secondo turno abbiamo le scommesse Z e W. Z ci dà 100 euro se esce una rossa o una gialla e W ci dà 100 euro se esce una nera o una gialla.
Le scelte sono razionali e transitive?
Secondo il principio di razionalità e transitività, nonché secondo la teoria del valore atteso, ci aspetteremmo di puntare su X al primo turno e su Z al secondo. Perché? Semplicemente perché conosciamo il numero di biglie rosse con esattezza ma non conosciamo quante delle altre siano nere e quante gialle: sappiamo solo che, in totale, sono 60. Il paradosso di Ellsberg ci mostra la violazione delle ipotesi base perché gli agenti sceglieranno X al primo turno, ma W al secondo. Questi sono i risultati di test sperimentali. Eppure, razionalmente, dovremmo scegliere W SE E SOLO SE la probabilità che esca una gialla o una nera fosse maggiore di pescare una rossa. Matematicamente si dimostra che il paradosso esiste e consiste nel giungere alla conclusione che, contemporaneamente, pescare una rossa è più probabile che pescare una biglia nera e pescare una nera sia più probabile che pescare una rossa.
