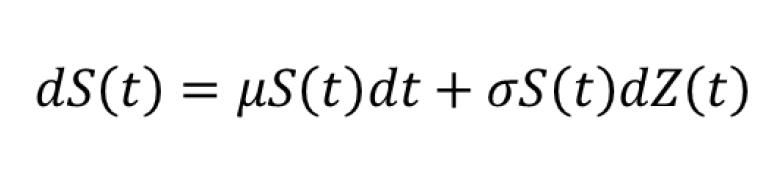Il modello Black-Scholes-Merton
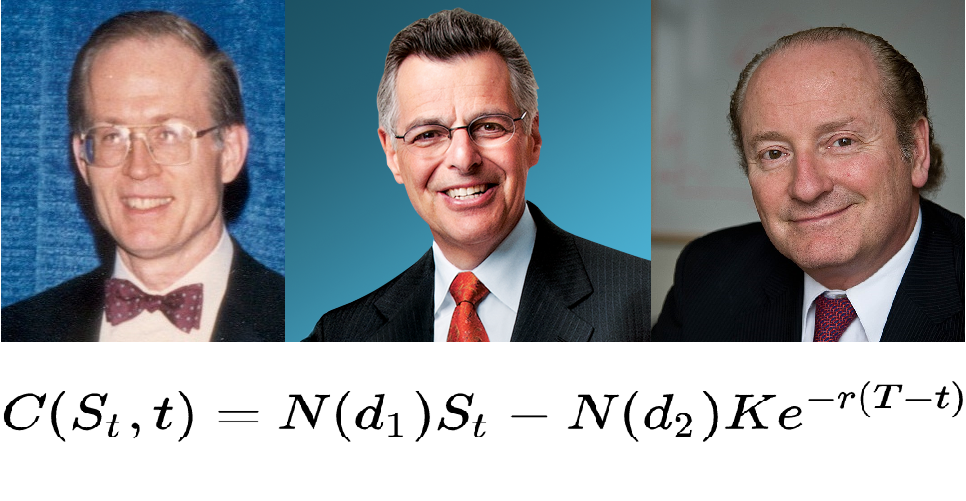
Black–Scholes–Merton
Il modello di Black-Scholes-Merton è di fondamentale importanza per l’analisi finanziaria dei mercati. Il modello MSM vide la luce con un famoso paper del 1973 e con questo i suddetti signori vinsero il premio Nobel nel 1997 (peccato per Mr. Black che morì nel 1995). Il paper ha come autori solo Black e Scholes ma i lavori precedenti di Merton hanno influito anche nell’assegnazione del Nobel.
Questo modello consente infatti, in condizioni di non arbitraggio, di determinare il prezzo di un’opzione PUT e di una CALL. In questo caso il non arbitraggio deriva dal fatto che l’investitore non dovrà ricevere un guadagno non spiegato da una componente di rischio.
Esempio pratico di non arbitraggio
Supponiamo di voler comprare una semplice opzione Call di tipo americano avente come sottostante Tesla, al momento della scrittura dell’articolo il prezzo di un’azione quota $ 376.79. Una call con strike 375 con scadenza a 4 giorni ha un ultimo prezzo di $ 5.15. Ciò vuol dire che, riservandoci il diritto di comprare a $ 375 qualcosa che attualmente quota $ 376.79 con $5.15, a quattro giorni il modello e l’analisi tecnica prevedono che il prezzo della tesla salirà a 375 + 5.15 = $380.15. O perlomeno è il prezzo più plausibile con il giusto rischio.
Le ipotesi del modello
Innanzitutto una grande precisazione. Nell’esempio ho mostrato un tipo di opzione americano. Quelle americane rispetto a quelle europee hanno un grande vantaggio: possono essere riscattate in qualsiasi momento. Quelle europee invece vanno tenute fino a scadenza. Nel modello BSM il tipo di opzione considerato è appunto quello europeo poiché più trattabile. Nel caso americano entra in gioco una variabile troppo casuale. Il tempo viene considerata inoltre una variabile continua e non discreta. Ma ecco un bell’elenco:
- Il mercato deve essere aperto in maniera continua, si possono cioè scambiare opzioni sempre;
- Il mercato è considerato perfetto così come nel modello CAPM (non ci sono costi di transazione e costi fiscali, i titoli infinitamente divisibili in parti, sono consentite vendite allo scoperto e gli agenti del mercato sono razionali massimizzatori del profitto);
- Sono esclusi gli arbitraggi non rischiosi (vige cioè il principio di assenza di arbitraggio);
- Sul mercato siano disponibili Zero Coupon Bond (ZCB) con scadenza qualsiasi e la struttura per scadenza è deterministica e piatta, ad un livello di intensità istantanea ad un interesse r fissato.
La genesi del modello
Il modello non è dei più semplici e presuppone la conoscenza della risoluzione di equazioni differenziali stocastiche e del moto Browniano, che descrive l’andamento casuale dei prezzi,così come la conoscenza della Heat Equation (equazione del calore). Per giusta conoscenza, questa è l’equazione del processo che descrive l’andamento del prezzo corrente S(t) in generale:
Dove:
- dt è un intervallo infinitesimo di tempo (ricordiamoci che lavoriamo nel continuo);
- dS(t) è di conseguenza la variazione infinitesima del prezzo corrente;
- μ è una costante che amano tutti i matematici, non può non esserci una costante in un processo stocastico. Essa rappresenta l’andamento medio dell’azione nell’intervallo infinitesimo. Dunque, il primo membro della parte destra μS(t)dt rappresenta il cosiddetto drift dell’equazione. Cioè quanto appunto “drifta” il prezzo nel tempo dt.
- σ è la volatilità istantanea del prezzo dell’azione. La quantità σS(t) (trattasi di quantità in quanto prezzo corrente moltiplicato per la volatilità) rappresenta il coefficiente di diffusione dell’equazione differenziale stocastica.
- dZ(t) è l’incremento infinitesimo subito dal moto Browninano (in alcune varianti il processo diventa di Wiener) nell’intervallo di tempo dt. Il moto Browninano standard considerato in questo caso è una successione di variabili casuali su t, distribuite secondo una normale standard N(0,1). Quindi il moto ha varianza dt e media 0.
La soluzione
La distribuzione finale S(t+τ) dove τ è il tempo successivo, sarà una lognormale con parametri (μ-σ^2/2)τ e σ*τ^1/2. Risolvendo si ottiene che:
Soluzione del processo dei prezzi.
Il modello vero e proprio
Ora bisogna costruire il prezzo delle opzioni. Mettiamo caso che vogliamo costruire un nostro portafoglio (Wallet, W) composto da una posizione lunga sull’opzione Call (C) e corta sull’azione (Stock, S):
W=C-ΔS
La variazione infinitesima del portafoglio è data da:
dW=dC-dΔS
Dobbiamo costruire questo portafoglio in modo che sia un portafoglio che ci protegga dal rischio (hedge portfolio) e sia tale che il suo rendimento sia pari al rendimento certo i (tasso risk free).
L’equazione generale, ceteris paribus (che belle parole) diventa:

Un’equazione differenziale del secondo ordine, con un constraint (condizione al contorno) che ha questa forma:

Chi ci segue e mastica un po’ di matematica sa già dove siamo arrivati. Questo sistema di equazione con condizione al contorno rappresenta, assieme alle condizioni iniziali, proprio l’Equazione del calore. La sua risoluzione rappresenta la soluzione finale al famoso modello.
Le soluzioni del modello

Qui davanti abbiamo la risoluzione per il prezzo della CALL, con d1 e d2 espresse. Soluzione derivante proprio dai calcoli un po’ macchinosi dell’equazione del calore.
Infine, per la soluzione per la PUT bisogna fare una piccola aggiunta. Sapendo che la formula deriva dall’equazione di parità che è la seguente:

E sostituendo C(t) con la soluzione della CALL che abbiamo trovato prima, ecco la soluzione finale della PUT

Così facendo abbiamo finalmente ottenuto ciò che volevamo: Due equazioni statiche che permettono in ogni momento di prezzare le opzioni Call e Put di tipo europeo sui mercati azionari.
La loro importanza è fuori da ogni discussione.