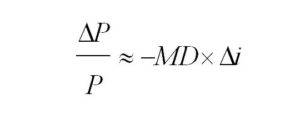La Duration – Conoscere il rischio obbligazionario

La Duration (in italiano “durata finanziaria”) è universalmente utilizzata come indicatore del livello di rischio di un titolo obbligazionario. La sua formulazione risale al 1938, anno in cui un illuminato economista canadese di nome Frederick Robertson Macaulay riuscì nell’intento di confezionare una elegante espressione matematica in grado di offrire una misura della rischiosità di un bond: la Macaulay Duration rappresenta ancora oggi una delle colonne portanti della Finanza, oltre che la base di pressochè tutta la modellistica inerente il mercato dei titoli a reddito fisso.
La sua caratteristica unica risiede nella capacità di sintetizzare il grado di sensibilità del valore di un’obbligazione al variare del tasso di interesse di mercato: ciò significa che, muovendo dalla duration, siamo in grado di quantificare l’impatto in termini di prezzo di una variazione dei tassi di mercato sul valore di un titolo.
Definizione e caratteristiche tecniche
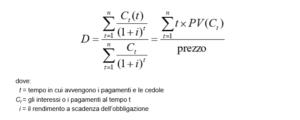
Dal punto di vista matematico l’indicatore rappresenta la scadenza media dei flussi di cassa di un titolo, ponderata per il valore attuale dei flussi (cioè il suo corso tel quel, ovvero il suo prezzo).
La Duration esprime dunque la “durata corretta in senso finanziario” di una obbligazione, ed è sempre minore della vita residua del titolo, eccezion fatta per i titoli privi di cedola per i quali i due valori sono identici. I titoli con durata finanziaria più elevata saranno dunque più rischiosi, in quanto più sensibili alle variazioni dei tassi di mercato. Oltre che della vita residua del titolo, la duration è funzione anche dell’entità dei pagamenti cedolari, in quanto a cedole maggiori corrisponde una duration minore (infatti assume valore massimo per gli ZCB), e del livello del tasso di rendimento, poiché diminuisce all’aumentare di quest’ultimo.
Il teorema dell’immunizzazione
Da ciò discende il fondamentale teorema dell’immunizzazione: l’acquisto di un titolo con duration pari al periodo di detenzione consente di ottenere un rendimento pari al TRES (tasso di riferimento effettivo a scadenza), ovvero il tasso di interesse del titolo. Questo avviene proprio in forza del fatto che un’eventuale variazione del prezzo di mercato di un titolo determinato da una modificazione del livello dei tassi, sarebbe compensata dal maggiore o minore rendimento determinato dal re-impiego dei flussi di cassa periodici. La validità del teorema dell’immunizzazione risulta limitata se applicata ad un singolo titolo, in quanto difficilmente un operatore investe solamente in titoli con duration esattamente pari all’orizzonte temporale di investimento desiderato. Il teorema diventa però facilmente applicabile ad un portafoglio di titoli la cui duration può essere manipolata attraverso una diversificazione per scadenze.
Il risultato del calcolo dell’indicatore rende dunque un risultato espresso in unità di tempo, solitamente anni, il quale rappresenta appunto la durata finanziaria del titolo: più alto è il valore dell’indicatore, maggiore è il rischio legato allo strumento. Ma come facciamo a valutare l’entità dell’impatto in termini di variazione di prezzo del titolo al variare dei tassi di mercato?
La Duration modificata
Al fine di operare una stima precisa di tale impatto ci serviamo della duration modificata (Modified Duration, MD), definita come dal rapporto duration/(1+TRES). La duration modificata è un importante parametro di sensibilità: essa permette di calcolare la variazione percentuale del prezzo di un’obbligazione in base alla variazione percentuale del TRES secondo la relazione:
Come si evince dal grafico la duration rappresenta la derivata prima della curva della relazione tra prezzo (asse delle ascisse) e rendimento (asse delle ordinate) di un titolo a reddito fisso. Proprio a causa di questa caratteristica quando calcoliamo la modified duration (cioè la variazione del prezzo in funzione della variazione dei tassi) operiamo uno spostamento lungo la retta della duration, anziché lungo la curva prezzo-rendimento. Ciò implica che la modified duration esprima uno stima ragionevolmente precisa in caso di variazioni contenute di tasso, ma in caso di variazioni in valore assoluto più marcate l’errore commesso diventa consistente. Inoltre l’errore risulterà più grande in presenza di una curvatura più accentuata.
Limitare gli errori di approssimazione: Convexity
Per limitare gli effetti di tale errore fisiologico di stima è stato introdotto un fattore di correzione detto convessità (convexity), che ne riduce sensibilmente la significatività. L’errore non viene del tutto eliminato in quanto la relazione prezzo rendimento, oltre ad essere curvilinea e convessa, è anche asimmetrica: in particolare all’aumentare del tasso diminuisce la velocità di riduzione del valore. Al contrario, al diminuire del prezzo, aumenta la velocità di aumento del rendimento. La convessità del titolo cresce all’aumentare della duration. Per quanto riguarda invece la relazione tra convessità e flussi di cassa, la prima sarà tanto più alta quanto meno i flussi di cassa sono concentrati attorno alla duration: gli ZCB sono infatti i titoli a convessità minore, in quanto non vi è dispersione dei flussi. La convessità è una proprietà desiderabile in quanto i titoli con curvatura più elevata esprimono escursioni di prezzo positive più marcate ed escursioni negative meno consistenti.